止于至善

0%

沙堆模型

发表于 分类于

沙堆模型（sandpile model）是根据一个简单的沙粒扩散规则来描述沙堆的累计和崩塌。当沙粒数量达到一定时，沙堆可呈现出明显的分形结构。除此之外，沙堆模型还包含很多有趣现象。

推荐阅读：The Amazing, Autotuning Sandpile、Sandgallery、Mommy Talk

规则

假设有一个无限大的正交网格，仅在某个固定格点处逐粒放沙。如下图所示，当某一格点中的沙粒的数量达到4时，这个格点发生崩塌，减去4颗沙粒，并将这4颗沙粒等分给上下左右的4个格点。

\[ \boxed{\begin{matrix} 0 & 0 & 0 \\ 0 & \textcolor{red}{4} & 0 \\ 0 & 0 & 0 \end{matrix}} \quad\Longrightarrow\quad \boxed{\begin{matrix} 0 & \textcolor{red}{1} & 0 \\ \textcolor{red}{1} & 0 & \textcolor{red}{1} \\ 0 & \textcolor{red}{1} & 0 \end{matrix}} \]

按照上面的规则，沙堆模型会在不断地累计与崩塌之间逐渐扩大。

分形

一百万粒沙

整个沙堆稳定后，格点中的沙粒数只有4个状态：3、2、1、0。将这四种状态分别用4种颜色代替，即：

三粒沙：亮红色，即RGB = #F40000 = [244,0,0]
两粒沙：橘黄色，即RGB = #FF7F00 = [255,127,0]
一粒沙：亮黄色，即RGB = #FFF200 = [255,255,32]
零粒沙：纯白色，即RGB = #FFFFFF = [255,255,255]

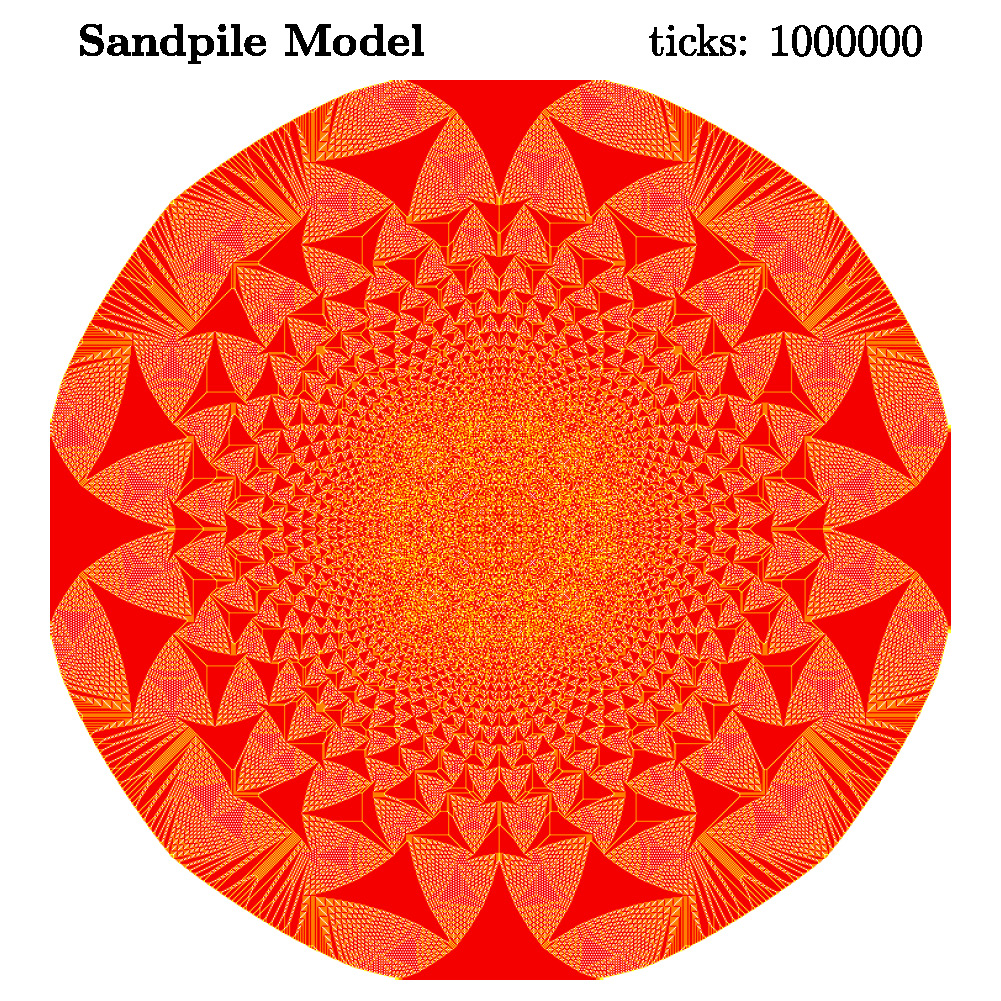
当落下一百万粒沙（\(10^6\)），沙堆累计的可视化过程如下

一百万粒沙的沙堆具有较明显的分形结构，沙堆效果如下

十亿粒沙

当落下十亿粒沙（\(10^9\)），具有很明显的分形效果，沙堆效果如下

上图来自Sandgallery

分析

分析一百万粒沙累计过程的数据。

格点总数-沙粒总数

  • 格点总数：沙堆所占区域的总格点数（包括内部零沙粒格点，但不包括外部零沙粒格点）

    十亿粒沙的沙堆图中蓝色部分为外部零沙粒格点

  • 沙粒总数：沙堆中沙粒的总数量

例如下图中的沙粒总数为7，格点总数为5。 \[ \boxed{\begin{matrix} & 1 & \\ 1 & 3 & 1 \\ & 1 & \end{matrix}} \]

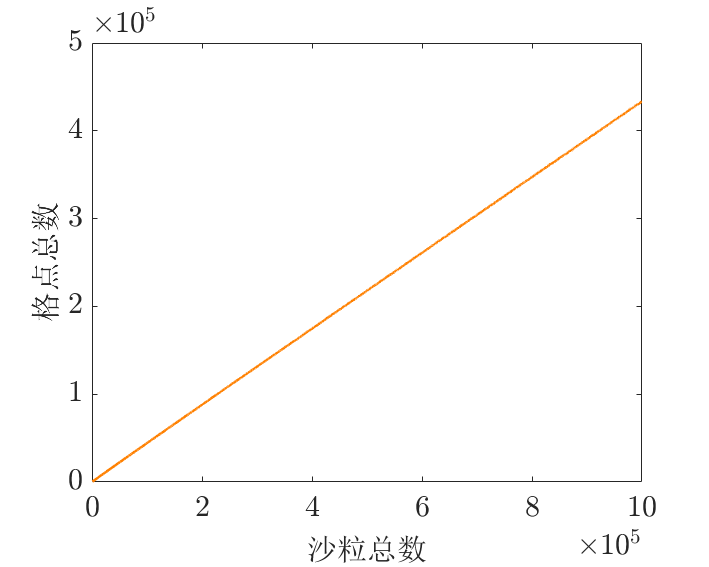
线性关系

单格平均沙粒数-沙粒总数

  • 单格平均沙粒数：沙粒总数 / 格点总数

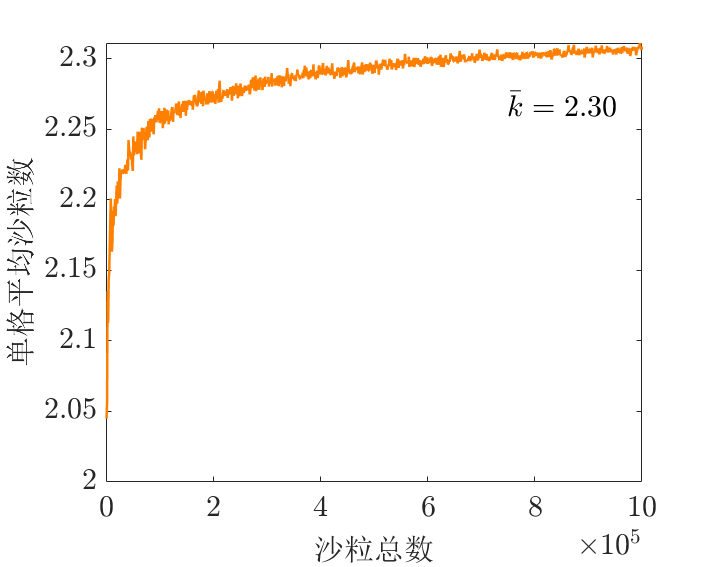
单格平均沙粒数稳定到2.30左右？

二八定律

沙堆的沙粒总数记为 \(M\)，格点总数记为 \(N\)，格点中沙粒数为 \(k\) 的格点共有 \(n\) 个，于是

  • 沙粒数为 \(k\) 的数量分布定义为 \(nk/M\)
  • 沙粒数为 \(k\) 的格点分布定义为 \(n/N\)

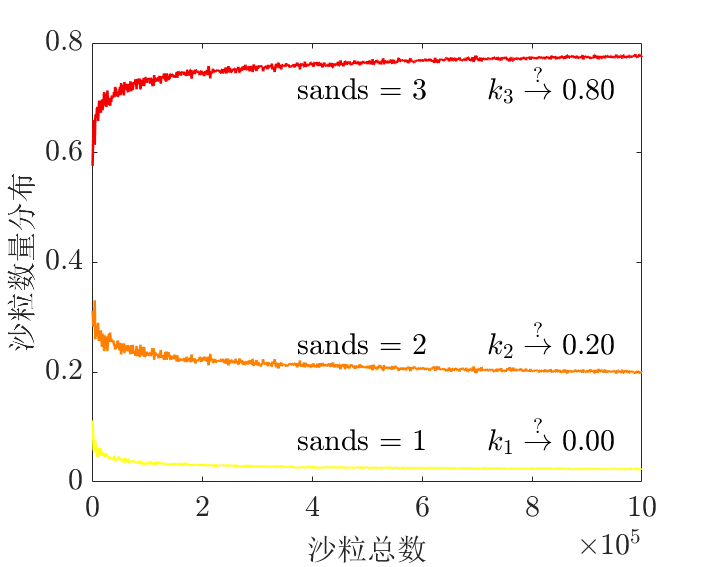
沙粒数为3的数量分布稳定到0.8左右？

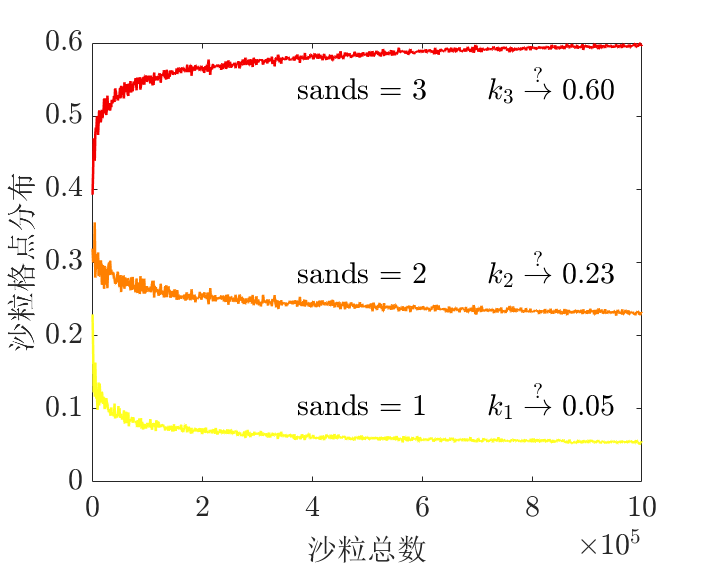
沙粒数为3的格点分布稳定到0.6左右？

二八定律是一个社会现象，其中一条是“20%的人掌握着80%的财富”。

对于本文所计算的一百万粒沙，对应为“60%的格点掌握着80%的沙粒”。

程序

MATLAB程序：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
%% 10^5颗沙粒的累计过程
% sandpile model
clc;clear;close all;

%% 沙粒个数
num1=10^5;

%% 初始化
dis=10^2;% 每dis颗沙粒保存一帧
pt=25;% 字体大小
L=1;% 正方形沙盘长度, 奇数格
center=ceil(L/2);% 沙盘中心坐标
sand=zeros(L,L);% 初始化沙盘, 全置零
color=[1.0000,1.0000,1.0000; % 纯白色
       1.0000,1.0000,0.1250; % 亮黄色
       1.0000,0.5000,0.0000; % 橘黄色
       0.9583,0.0000,0.0000];% 亮红色
index=1;

%% 每帧图片
frames(num1/dis)=struct('cdata',[],'colormap',[]);

%% 逐粒放沙
for i=1:num1
    sand(center,center)=sand(center,center)+1;
    [tempi,tempj]=find(sand>=4);% 大于3的位置
    num2=length(tempi);
    while num2>0
        for j=1:num2
            
           %% 防止溢出
            if tempi(j)==1 || tempi(j)==L || tempj(j)==1 || tempj(j)==L
                % 四周加一圈零
                sand=[         0, zeros(1,L),          0;
                      zeros(L,1),       sand, zeros(L,1);
                               0, zeros(1,L),          0];
                L=L+2;center=center+1;
                tempi=tempi+1;tempj=tempj+1; 
            end
            
           %% 沙堆崩塌
            sand(tempi(j),tempj(j))=sand(tempi(j),tempj(j))-4;
            sand(tempi(j)+1,tempj(j))=sand(tempi(j)+1,tempj(j))+1;
            sand(tempi(j)-1,tempj(j))=sand(tempi(j)-1,tempj(j))+1;
            sand(tempi(j),tempj(j)+1)=sand(tempi(j),tempj(j)+1)+1;
            sand(tempi(j),tempj(j)-1)=sand(tempi(j),tempj(j)-1)+1;
            
        end
        [tempi,tempj]=find(sand>=4);% 大于3的位置
        num2=length(tempi);
    end
    
    if mod(i,dis)==0
        imshow(sand,[0,3],'Colormap',color);
        figset([20,20,0.3,0.02],[0.9,0.9,0.05,0.02]);
        
        str1='\bf{Sandpile Model}';h1=text(0,0,str1);
        set(h1,'interpreter','latex','HorizontalAlignment','left');
        set(h1,'units','normalized','fontsize',pt,'position',[0.03,1.04]);
        
        str2=['ticks: ',sprintf('%d',i)];h2=text(0,0,str2);
        set(h2,'interpreter','latex','HorizontalAlignment','right');
        set(h2,'units','normalized','fontsize',pt,'position',[0.97,1.04]);
        
        drawnow;
        frames(index)=getframe(gcf);
        index=index+1;
    end
end

%% 视频
v=VideoWriter('newfile.mp4','MPEG-4');
v.Quality=100;v.FrameRate=30;
open(v);
writeVideo(v,frames);
close(v);

%% 设置图像尺寸与位置
function figset(parameter1,parameter2)

    %电脑屏幕尺寸
    set(0,'units','centimeters')
    cm_ss=get(0,'screensize');
    W=cm_ss(3);%电脑屏幕长度，单位cm
    H=cm_ss(4);%电脑屏幕宽度，单位cm

	%设置figure在screen中的比例位置与大小
	temp1=[parameter1(3),parameter1(4),parameter1(1)/W,parameter1(2)/H];
    set(gcf,'units','normalized','position',temp1);
    if nargin==2
		%设置axis在figure中的比例位置与大小
		temp2=[parameter2(3),parameter2(4),parameter2(1),parameter2(2)];
        set(gca,'position',temp2);
    end

end