相场损伤模型

基于相场法的损伤模型主要用于研究裂纹的扩展演化问题。

裂纹的扩散拓扑

图1 尖锐裂纹与扩散拓扑裂纹：

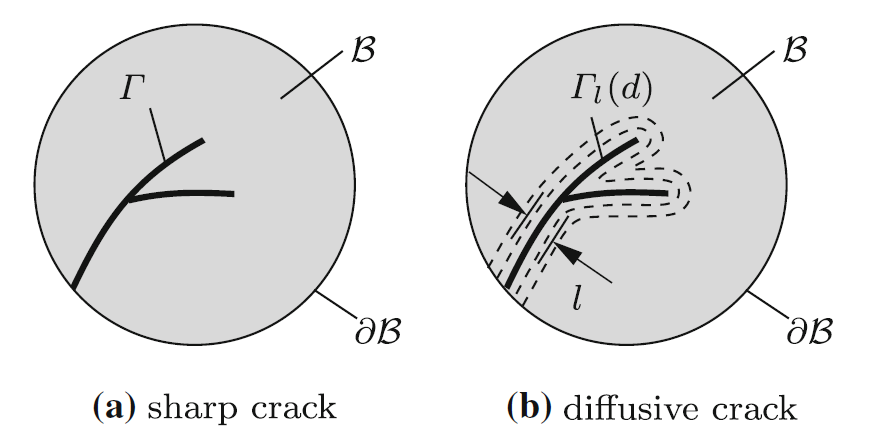
图2 尖锐裂纹与扩散裂纹模型：

尖锐裂纹可以采用一个辅助的场变量 \(d\) 来描述，即

\[ \tag{1} d(x)=\begin{cases} 1&x=0\\[5pt] 0&x\neq0 \end{cases} \]

显然，\(d=0\) 对应未断裂状态，\(d=1\) 则对应完全断裂状态。将这个辅助场变量 \(d(x)\) 称为裂纹相场。裂纹相场与连续损伤力学相关，因为连续损伤力学中的标量损伤度 \(d\) 在宏观层面上描述了微裂纹和微孔洞的均匀化发展。为了改善式(1)中相场的非连续性，可以采用指数模型，即

\[ \tag{2a} d(x)=\mathrm{e}^{-|x|/l} \]

\[ \tag{2b} d(0)=1~,~d(\pm\infty)=0 \]

式(2)即表示了裂纹的扩散拓扑（正则化），其函数图像如图2(b)所示。裂纹的扩散拓扑程度由长度尺度参数 \(l\) 控制，当 \(l\to 0\) 时，式(2)等价于式(1)。

能量耗散密度函数

考虑如下的齐次微分方程

\[ \tag{3} d(x)-l^2d''(x)=0 \]

注意到式(2)是上式的一个解，而该微分方程是下面变分问题的欧拉方程

\[ \tag{4} \min_{d(x)} ~I(d)=\frac{1}{2}\int_{V}\big(d^2+l^2d'^2\big)\mathrm{d}v \]

这里引入泛函的目的有两个：1、定义能量耗散密度函数，2、推导裂纹相场的控制方程

令 \(\mathrm{d}v=\Gamma\mathrm{d}x\) ，于是有

\[ \tag{5} I(d=\mathrm{e}^{-|x|/l})=\Gamma\int_{-\infty}^{+\infty}\mathrm{e}^{-2|x|/l}\mathrm{d}x=l\Gamma\int_0^{+\infty}\mathrm{e}^{-2x/l}\mathrm{d}(-2x/l)=l\Gamma \]

由此引入能量耗散函数 \(\Gamma_l\) 与能量耗散密度函数 \(\gamma\)

\[ \tag{6a} \Gamma_l(d)=\frac{1}{l}I(d)=\int_{V}\gamma~\mathrm{d}v \]

\[ \tag{6b} \gamma(d)=\frac{1}{2l}\big(d^2+l^2d'^2\big) \]

能量耗散函数 \(\Gamma_l\) 是关于裂纹相场 \(d(x)\) 的泛函。将式(6)中的一维形式推广到多维，即

\[ \tag{7a} \Gamma_l(d,\nabla d)=\int_{V}\gamma~\mathrm{d}v \]

\[ \tag{7b} \gamma(d,\nabla d)=\frac{1}{2l}\big(d^2+l^2\nabla d\cdot\nabla d\big) \]

此时裂纹相场 \(d(\boldsymbol{x})\) 是关于空间位置坐标 \(\boldsymbol{x}\) 的函数。

裂纹相场的控制方程

求式(7)中能量耗散函数的变分问题，即

\[ \tag{8} \min_{d(\boldsymbol{x})} ~\Gamma_l(d)=\frac{1}{2l}\int_{V}\big(d^2+l^2\nabla d\cdot\nabla d\big)\mathrm{d}v \]

取能量耗散函数的变分，即

\[ \tag{9} \begin{aligned} \delta\Gamma_l(d,\nabla d)&=\int_V\bigg(\frac{\partial\gamma}{\partial d}\delta d+\frac{\partial\gamma}{\partial\nabla d}\cdot\delta\nabla d\bigg)\mathrm{d}v\\[8pt] &=\frac{1}{l}\int_{V}\big[d\delta d+l^2\underbrace{\nabla d}_{u}\cdot\underbrace{\delta\nabla d}_{v'}\big]\mathrm{d}v\\[1pt] &=\frac{1}{l}\bigg[\int_Vd\delta d\mathrm{d}v+\underbrace{l^2\nabla d\cdot\boldsymbol{n}\delta d\bigg|_{\partial V}-\int_Vl^2\overbrace{\nabla\cdot(\nabla d)}^{\nabla^2d=\Delta d}\delta d\mathrm{d}v}_{\text{分部积分}}\bigg]\\[1pt] &=\frac{1}{l}\int_V(d-l^2\Delta d)\delta d\mathrm{d}v+l\nabla d\cdot\boldsymbol{n}\delta d\bigg|_{\partial V} \end{aligned} \]

分部积分公式：\(\displaystyle\int uv'\mathrm{d}x=uv-\int u'v\mathrm{d}x\)

导数的变分等于变分的导数：\(\delta\nabla d=\nabla\delta d\)

显然变分 \(\delta\Gamma_l=0\) 的充分条件为

是否为必要条件？我不知道

\[ \tag{10} \begin{cases} d-l^2\Delta d=0&~\mathrm{in}~V\\[5pt] \nabla d\cdot\boldsymbol{n}=0&~\mathrm{on}~\partial V \end{cases} \]

式中，\(\boldsymbol{n}\) 为自然边界 \(\partial V\) 的外法线矢量。同时裂纹相场还需满足强制边界条件

\[ \tag{11} d(\boldsymbol{x})=1\quad\mathrm{on}~\Gamma \]

式中，\(\Gamma\) 表示一维的开裂点、二维的裂纹线、三维的裂纹面。

综上，裂纹相场的控制方程为

\[ \tag{12} \begin{cases} d-l^2\Delta d=0&~\mathrm{in}~V\\[5pt] \nabla d\cdot\boldsymbol{n}=0&~\mathrm{on}~\partial V\\[5pt] d(\boldsymbol{x})=1&~\mathrm{on}~\Gamma \end{cases} \]

实际上，式(12)给定了椭圆型的偏微分方程、Neumann边界条件以及Dirichlet边界条件，该控制方程描述了裂纹相场的定常状态。

MATLAB的pdetool工具箱支持求解二维的椭圆型、抛物型、双曲型以及特征值模式的偏微分方程，求解方法为有限元法。在pdetool工具箱中椭圆型偏微分方程定义为

\[ \tag{13} au-c\Delta u=f \]

按照式(12)，令 \(a=1/l^2\)、\(c=1\)、\(f=0\) 即可。图3展示了求解域为 \(2\times2\) 的正方形，裂纹长度为 \(1\)，长度尺度参数 \(l=0.25\) 的相场解。

图3 裂纹相场：

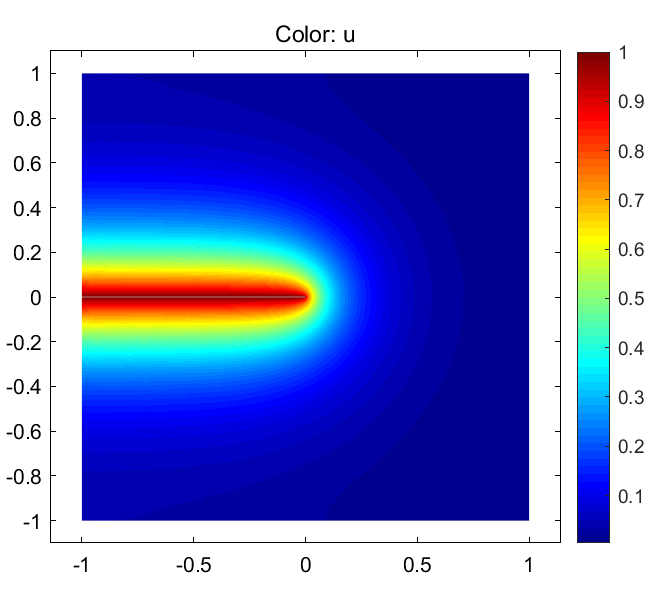
由pdetool工具箱生成的代码如下：

function pde_phase_field_damage_line
[fig,ax]=pdeinit;
pdetool('appl_cb',1);set(ax,'DataAspectRatio',[1 1 1]);
set(ax,'PlotBoxAspectRatio',[730.45 486 486]);
set(ax,'XLimMode','auto');set(ax,'YLim',[-1 1]);
set(ax,'XTickMode','auto');set(ax,'YTickMode','auto');

% Geometry description:
pderect([0 1 1 -1],'R1');pderect([-1 0 1 0.001],'R2');
pderect([-1 0 -0.0010000000000000009 -1],'R3');
set(findobj(get(fig,'Children'),'Tag','PDEEval'),'String','R1+R2+R3')

% Boundary conditions:
pdetool('changemode',0)
pdesetbd(12,'neu',1,'0','0');pdesetbd(11,'neu',1,'0','0');
pdesetbd(10,'neu',1,'0','0');pdesetbd(9,'neu',1,'0','0');
pdesetbd(7,'dir',1,'1','1');pdesetbd(5,'neu',1,'0','0');
pdesetbd(4,'neu',1,'0','0');pdesetbd(3,'dir',1,'1','1');
pdesetbd(2,'dir',1,'1','1');pdesetbd(1,'neu',1,'0','0');

% Mesh generation:
setappdata(fig,'Hgrad',1.3);
setappdata(fig,'refinemethod','regular');
setappdata(fig,'jiggle',char('on','mean',''));
setappdata(fig,'MesherVersion','preR2013a');
pdetool('initmesh');pdetool('refine');

% PDE coefficients:
pdeseteq(1,'1','16','0','1','0:10','0','0','[0 100]');
setappdata(fig,'currparam',['1.0';'10 ';'0  ';'1.0']);

% Solve parameters:
setappdata(fig,'solveparam',char('0','6570','10','pdeadworst',...
'0.5','longest','0','1E-4','','fixed','Inf'));

% Plotflags and user data strings:
setappdata(fig,'plotflags',[1 1 1 1 1 1 7 1 0 0 0 1 1 0 0 0 0 1]);
setappdata(fig,'colstring','');setappdata(fig,'arrowstring','');
setappdata(fig,'deformstring','');setappdata(fig,'heightstring','');

% Solve PDE:
pdetool('solve')

裂纹扩展的变分原理

考虑由裂纹相场引起的能量耗散，构造总势能泛函，当泛函的变分为零时，泛函取得极值，此时连续体处于平衡状态，即最小势能原理。

连续体的总势能由应变能、动能、耗散势能、载荷势能组成，即

\[ \tag{14} \underbrace{\Pi(\boldsymbol{u},\dot{\boldsymbol{u}},\boldsymbol{\varepsilon},d,\nabla d)}_{\text{总势能}}=\underbrace{E(\boldsymbol{\varepsilon},d)}_{\text{应变能}}+\underbrace{D(d,\nabla d)}_{\text{耗散势能}}+\underbrace{K(\dot{\boldsymbol{u}})}_{\text{动能}}-\underbrace{W(\boldsymbol{u})}_{\text{载荷势能}} \]

于是总势能的变分为

\[ \tag{15} \delta\Pi=\delta E+\delta D+\delta K-\delta W=0 \]

应变能的变分

对于没有裂纹（损伤）的各向同性线弹性材料，其应变能密度为

\[ \tag{16} \psi(\boldsymbol{\varepsilon})=\mu\boldsymbol{\varepsilon}:\boldsymbol{\varepsilon}+\frac{1}{2}\lambda\mathrm{tr}^2(\boldsymbol{\varepsilon}) \]

其应力为

\[ \tag{17} \boldsymbol{\sigma}=\frac{\partial \psi(\boldsymbol{\varepsilon})}{\partial \boldsymbol{\varepsilon}}=2\mu\boldsymbol{\varepsilon}+\lambda\mathrm{tr}(\boldsymbol{\varepsilon})\boldsymbol{I} \]

式(17)的证明较为容易，将式(16)展开后再对 \(\varepsilon_{ij}\) 求导即可

由于裂纹的存在，必然导致材料力学性能的退化，于是可以定义退化后的应变能密度

\[ \tag{18a} \tilde{\psi}(\boldsymbol{\varepsilon},d)=\big[g(d)+k\big]\psi^+(\boldsymbol{\varepsilon})+\psi^-(\boldsymbol{\varepsilon}) \]

式中，\(g(d)\) 为退化函数，需满足 \(g(0)=1\) 、\(g(1)=0\) ；\(k\) 为正的小量，其作用为防止 \(d=1\) 时能量的完全退化导致刚度矩阵奇异；\(\psi^+(\boldsymbol{\varepsilon})\) 、\(\psi^-(\boldsymbol{\varepsilon})\) 分别表示由拉伸、压缩主导的应变能密度，且需要满足下式

\[ \tag{18b} \psi(\boldsymbol{\varepsilon})=\psi^+(\boldsymbol{\varepsilon})+\psi^-(\boldsymbol{\varepsilon}) \]

式(18a)表明仅考虑拉伸引起的损伤（裂纹开裂），这也反映了各向异性的性能退化。退化函数的选取，以及应变能密度的拉伸、压缩分解将在后续进行讨论。

将式(18a)在求解域 \(V\) 上积分，可得连续体的应变能

\[ \tag{19} E(\boldsymbol{\varepsilon},d)=\int_V\tilde{\psi}(\boldsymbol{\varepsilon},d)\mathrm{d}v \]

于是应变能的变分为

\[ \tag{20} \begin{aligned} \delta E(\boldsymbol{\varepsilon},d)&=\int_V\bigg(\frac{\partial \tilde{\psi}}{\partial \boldsymbol{\varepsilon}}:\delta\boldsymbol{\varepsilon}+\frac{\partial \tilde{\psi}}{\partial d}\delta d\bigg)\mathrm{d}v\\[8pt] &=\int_V\Big\{\big[g(d)+k\big]\partial_\boldsymbol{\varepsilon}\psi^++\partial_\boldsymbol{\varepsilon}\psi^-\Big\}:\delta\boldsymbol{\varepsilon}\mathrm{d}v+\int_Vg'(d)\psi^+\delta d\mathrm{d}v \end{aligned} \]

耗散势的变分

耗散势通过对耗散势密度函数在求解域 \(V\) 上积分得到，即

\[ \tag{21a} D(d,\nabla d)=\int_V\varphi(d,\nabla d)\mathrm{d}v \]

式中，耗散势密度函数的定义为

\[ \tag{21b} \varphi(d,\nabla d)=g_c\gamma(d,\nabla d) \]

式中，\(g_c\) 为材料参数（为了统一量纲）。于是由式(7)可得

\[ \tag{22} D(d,\nabla d)=g_c\Gamma_l(d,\nabla d) \]

于是根据式(9)可得

\[ \tag{23} \delta D(d,\nabla d)=g_c\delta\Gamma_l(d,\nabla d)=\frac{g_c}{l}\int_V(d-l^2\Delta d)\delta d\mathrm{d}v+g_cl\nabla d\cdot\boldsymbol{n}\delta d\bigg|_{\partial V} \]

动能与载荷势能的变分

动能的定义

\[ \tag{24a} K(\dot{\boldsymbol{u}})=\int_V\frac{1}{2}\rho\dot{\boldsymbol{u}}\cdot\dot{\boldsymbol{u}}\mathrm{d}v \]

载荷势能的定义

\[ \tag{24b} W(\boldsymbol{u})=\int_V \boldsymbol{b}\cdot\boldsymbol{u}\mathrm{d}v+\oint_{\partial V}\boldsymbol{t}\cdot\boldsymbol{u}\mathrm{d}s \]

载荷势能并不等于载荷所作的功

在《弹性体的应变能密度》中给出动能与载荷势能的变分，即

\[ \tag{25a} \delta K=\int_V\rho\ddot{\boldsymbol{u}}\cdot\delta\boldsymbol{u}\mathrm{d}v \]

\[ \tag{25b} \delta W=\int_V(\nabla\cdot\boldsymbol{\sigma}+\boldsymbol{b})\cdot\delta\boldsymbol{u}\mathrm{d}v+\int_V\boldsymbol{\sigma}:\delta\boldsymbol{\varepsilon}\mathrm{d}v \]

耦合方程

于是由将式(20)、(23)、(25)代入式(15)可得总势能变分

\[ \tag{26} \begin{aligned} \delta\Pi=&~\delta E+\delta D+\delta K-\delta W\\[5pt] =&~\int_V(\rho\ddot{\boldsymbol{u}}-\nabla\cdot\boldsymbol{\sigma}-\boldsymbol{b})\cdot\delta\boldsymbol{u}\mathrm{d}v+\int_V\Big[\frac{g_c}{l}(d-l^2\Delta d)+g'(d)\psi^+\Big]\delta d\mathrm{d}v+~\\[8pt] &~\int_V\Big\{\big[g(d)+k\big]\partial_\boldsymbol{\varepsilon}\psi^++\partial_\boldsymbol{\varepsilon}\psi^--\boldsymbol{\sigma}\Big\}:\delta\boldsymbol{\varepsilon}\mathrm{d}v+g_cl\nabla d\cdot\boldsymbol{n}\delta d\bigg|_{\partial V}=0 \end{aligned} \]

显然变分 \(\delta\Pi=0\) 的充分条件为

\[ \tag{27} \begin{cases} \nabla\cdot\boldsymbol{\sigma}+\boldsymbol{b}=\rho\ddot{\boldsymbol{u}}\\[5pt] \displaystyle\frac{g_c}{l}(d-l^2\Delta d)=-g'(d)\psi^+\\[5pt] \boldsymbol{\sigma}=\big[g(d)+k\big]\partial_\boldsymbol{\varepsilon}\psi^++\partial_\boldsymbol{\varepsilon}\psi^- \end{cases} \]

为了体现损伤的不可逆性，即 \(\dot{d}\ge0\)，引入能量历史最大函数

\[ \tag{28} \mathcal{H}(\boldsymbol{\varepsilon})=\max_{t\in[0,t_\mathrm{f}]}\psi^+(\boldsymbol{\varepsilon};t) \]

耗散势变分 \(\delta D\ge0\)，仅需 \(-g'(d)\psi^+\ge0\) 即可，而 \(\psi^+\) 肯定是不小于零

所以引入 \(\mathcal{H}(\boldsymbol{\varepsilon})\)，不是很懂

于是，将式(27)改写为

\[ \tag{29a} \begin{cases} \nabla\cdot\boldsymbol{\sigma}+\boldsymbol{b}=\rho\ddot{\boldsymbol{u}}\\[5pt] \displaystyle\frac{g_c}{l}(d-l^2\Delta d)=-g'(d)\mathcal{H}\\[5pt] \boldsymbol{\sigma}=\big[g(d)+k\big]\partial_\boldsymbol{\varepsilon}\psi^++\partial_\boldsymbol{\varepsilon}\psi^- \end{cases} \]

式(29a)是耦合损伤的平衡方程与裂纹相场方程。相应的自然边界条件为

\[ \tag{29b} \begin{cases} \boldsymbol{n}\cdot\boldsymbol{\sigma}=\boldsymbol{t}&~\mathrm{on}~\partial V\\[5pt] \nabla d\cdot\boldsymbol{n}=0&~\mathrm{on}~\partial V \end{cases} \]

式(25b)的推导过程中使用了应力边界条件 \(\boldsymbol{n}\cdot\boldsymbol{\sigma}=\boldsymbol{t}\)

应变能密度的退化

这里具体讨论式(18a)中的退化函数 \(g(d)\) 以及拉伸、压缩应变能密度 \(\psi^+(\boldsymbol{\varepsilon})\) 、\(\psi^-(\boldsymbol{\varepsilon})\) 。

退化函数

退化函数 \(g(d)\) 首先需满足

\[ \tag{30a} \begin{cases} g(0)=1\\[5pt] g(1)=0 \end{cases} \]

这两种情况分别对应无裂纹时应变能没有退化、开裂时拉伸应变能完全退化。

考虑到式(27)或式(29b)中的第二个式子，当 \(d=1\) 时，为了保证弹性驱动力 \(\partial_d\tilde{\psi}=g'(d)\psi^+\) 收敛到一个有限值¹，于是令

\[ \tag{30b} g'(1)=0 \]

文献[1]里这样解释的，我是没看懂

于是在式(30)的条件下选取退化函数，例如

\[ \tag{31} g(d)=(1-d)^2 \]

应变能密度的拉压分解

首先定义两个算符

\[ \tag{32} \begin{cases} \langle x\rangle_+=(x+|x|)/2\\[5pt] \langle x\rangle_-=(x-|x|)/2 \end{cases} \]

为了方便展示，再将应变能密度函数给出

\[ \tag*{[16]} \psi(\boldsymbol{\varepsilon})=\mu\boldsymbol{\varepsilon}:\boldsymbol{\varepsilon}+\frac{1}{2}\lambda\mathrm{tr}^2(\boldsymbol{\varepsilon}) \]

分解形式1

文献[2]中将应变张量 \(\boldsymbol{\varepsilon}\) 进行谱分解，即

\[ \tag{33a} \boldsymbol{\varepsilon}=\sum_{i=1}^3 \varepsilon_i\boldsymbol{n}_i\otimes\boldsymbol{n}_i \]

式中，\(\varepsilon_i\)、\(\boldsymbol{n}_i\) 分别为应变张量 \(\boldsymbol{\varepsilon}\) 的第 \(i\) 个主应变、主方向，且 \(\|\boldsymbol{n}_i\|=1\) 。特别地，令 \(\boldsymbol{n}_i\) 均为列向量，记 \(\boldsymbol{Q}=[\boldsymbol{n}_1,\boldsymbol{n}_2,\boldsymbol{n}_3]\) ，则有

\[ \tag{33b} \mathrm{diag}([\varepsilon_1,\varepsilon_2,\varepsilon_3])=\boldsymbol{Q}^\mathrm{T}\cdot\boldsymbol{\varepsilon}\cdot\boldsymbol{Q} \]

实对称矩阵的谱分解性质

式中，\(\mathrm{diag}([\varepsilon_1,\varepsilon_2,\varepsilon_3])\) 表示主对角线元素为 \([\varepsilon_1,\varepsilon_2,\varepsilon_3]\) 的对角阵。事实上 \(\boldsymbol{Q}\) 为正交矩阵，式(33b)表示应变张量 \(\boldsymbol{\varepsilon}\) 经正交矩阵 \(\boldsymbol{Q}\) 旋转后得到主应变微体。

于是，在谱分解的基础上定义拉伸应变张量 \(\boldsymbol{\varepsilon}^+\) 与压缩应变张量 \(\boldsymbol{\varepsilon}^-\)

\[ \tag{34} \begin{cases} \boldsymbol{\varepsilon}^+=\sum_{i=1}^3 \langle\varepsilon_i\rangle_+\boldsymbol{n}_i\otimes\boldsymbol{n}_i\\[5pt] \boldsymbol{\varepsilon}^-=\sum_{i=1}^3 \langle\varepsilon_i\rangle_-\boldsymbol{n}_i\otimes\boldsymbol{n}_i \end{cases} \]

显然，对于式(34)所定义拉伸、压缩应变张量，恒有 \(\boldsymbol{\varepsilon}=\boldsymbol{\varepsilon}^++\boldsymbol{\varepsilon}^-\) 。

进一步可以定义拉伸、压缩应变能密度

\[ \tag{35} \begin{cases} \psi^+(\boldsymbol{\varepsilon})=\mu\boldsymbol{\varepsilon}^+:\boldsymbol{\varepsilon}^++\displaystyle\frac{1}{2}\lambda\langle\mathrm{tr}(\boldsymbol{\varepsilon})\rangle^2_+\\[5pt] \psi^-(\boldsymbol{\varepsilon})=\mu\boldsymbol{\varepsilon}^-:\boldsymbol{\varepsilon}^-+\displaystyle\frac{1}{2}\lambda\langle\mathrm{tr}(\boldsymbol{\varepsilon})\rangle^2_- \end{cases} \]

证明1

还需证明式(35)满足式(18b)。不难证明

\[ \mathrm{tr}^2(\boldsymbol{\varepsilon})=\langle\mathrm{tr}(\boldsymbol{\varepsilon})\rangle^2_++\langle\mathrm{tr}(\boldsymbol{\varepsilon})\rangle^2_- \]

因此还需证明

\[ \boldsymbol{\varepsilon}:\boldsymbol{\varepsilon}=\boldsymbol{\varepsilon}^+:\boldsymbol{\varepsilon}^++\boldsymbol{\varepsilon}^-:\boldsymbol{\varepsilon}^- \]

这里先证明两个子结论：令一阶张量 \(\boldsymbol{m}\)、\(\boldsymbol{n}\) 满足 \(\|\boldsymbol{m}\|=\|\boldsymbol{n}\|=1\) ，且 \(\boldsymbol{m}\cdot\boldsymbol{n}=0\) ，于是有

\[ \tag{36a} (\boldsymbol{n}\otimes\boldsymbol{n}):(\boldsymbol{n}\otimes\boldsymbol{n})=n_in_jn_in_j=\sum_i\Big[n_i^2\big(\sum_jn_j^2\big)\Big]=1 \]

\[ \tag{36b} (\boldsymbol{n}\otimes\boldsymbol{n}):(\boldsymbol{m}\otimes\boldsymbol{m})=n_in_jm_im_j=\sum_i\Big[n_im_i\big(\sum_jn_jm_j\big)\Big]=0 \]

于是根据式(36)，可得

\[ \tag{37a} \boldsymbol{\varepsilon}:\boldsymbol{\varepsilon}=\Big(\sum_{i=1}^3 \varepsilon_i\boldsymbol{n}_i\otimes\boldsymbol{n}_i\Big):\Big(\sum_{i=1}^3 \varepsilon_i\boldsymbol{n}_i\otimes\boldsymbol{n}_i\Big)=\sum_{i=1}^3\varepsilon_i^2 \]

\[ \tag{37b} \boldsymbol{\varepsilon}^+:\boldsymbol{\varepsilon}^+=\Big(\sum_{i=1}^3 \langle\varepsilon_i\rangle_+\boldsymbol{n}_i\otimes\boldsymbol{n}_i\Big):\Big(\sum_{i=1}^3 \langle\varepsilon_i\rangle_+\boldsymbol{n}_i\otimes\boldsymbol{n}_i\Big)=\sum_{i=1}^3\langle\varepsilon_i\rangle_+^2 \]

\[ \tag{37c} \boldsymbol{\varepsilon}^-:\boldsymbol{\varepsilon}^-=\Big(\sum_{i=1}^3 \langle\varepsilon_i\rangle_-\boldsymbol{n}_i\otimes\boldsymbol{n}_i\Big):\Big(\sum_{i=1}^3 \langle\varepsilon_i\rangle_-\boldsymbol{n}_i\otimes\boldsymbol{n}_i\Big)=\sum_{i=1}^3\langle\varepsilon_i\rangle_-^2 \]

进一步可得

\[ \tag{38} \boldsymbol{\varepsilon}^+:\boldsymbol{\varepsilon}^++\boldsymbol{\varepsilon}^-:\boldsymbol{\varepsilon}^-=\sum_{i=1}^3\varepsilon_i^2 \]

由式(37a)、(38)即可证明 \(\boldsymbol{\varepsilon}:\boldsymbol{\varepsilon}=\boldsymbol{\varepsilon}^+:\boldsymbol{\varepsilon}^++\boldsymbol{\varepsilon}^-:\boldsymbol{\varepsilon}^-\) 。

综上，由式(35)所定义的拉伸、压缩应变能密度满足式(18b)。

需要注意，直接将式(34)所定义的拉伸、压缩应变 \(\boldsymbol{\varepsilon}^+\)、\(\boldsymbol{\varepsilon}^-\) 代入式(16)，令 \[ \begin{cases} \psi^+=\psi(\boldsymbol{\varepsilon}^+)=\mu\boldsymbol{\varepsilon}^+:\boldsymbol{\varepsilon}^++\displaystyle\frac{1}{2}\lambda\mathrm{tr}^2(\boldsymbol{\varepsilon}^+)\\[5pt] \psi^-=\psi(\boldsymbol{\varepsilon}^-)=\mu\boldsymbol{\varepsilon}^-:\boldsymbol{\varepsilon}^-+\displaystyle\frac{1}{2}\lambda\mathrm{tr}^2(\boldsymbol{\varepsilon}^-) \end{cases} \] 这显然不能满足式(18b)。

偏导数1

由式(27)或式(29b)中的第三个式子可知，还需 \(\psi^+\)、\(\psi^-\) 对 \(\boldsymbol{\varepsilon}\) 的偏导数 \(\partial_\boldsymbol{\varepsilon}\psi^+\) 、\(\partial_\boldsymbol{\varepsilon}\psi^-\) 。于是由式(35)可得

\[ \tag{39} \begin{cases} \partial_\boldsymbol{\varepsilon}\psi^+=2\mu\boldsymbol{\varepsilon}^++\lambda\langle\mathrm{tr}(\boldsymbol{\varepsilon})\rangle_+\boldsymbol{I}\\[5pt] \partial_\boldsymbol{\varepsilon}\psi^-=2\mu\boldsymbol{\varepsilon}^-+\lambda\langle\mathrm{tr}(\boldsymbol{\varepsilon})\rangle_-\boldsymbol{I} \end{cases} \]

这个不知道怎么证明

分解形式2

文献[1]中采用主应变形式的应变能密度，即

\[ \tag{40} \psi(\varepsilon_1,\varepsilon_2,\varepsilon_3)=\mu(\varepsilon_1^2+\varepsilon_2^2+\varepsilon_3^2)+\frac{1}{2}\lambda(\varepsilon_1+\varepsilon_2+\varepsilon_3)^2 \]

相应的拉伸、压缩应变能密度定义为

\[ \tag{41} \psi^\pm=\mu(\langle\varepsilon_1\rangle_\pm^2+\langle\varepsilon_2\rangle_\pm^2+\langle\varepsilon_3\rangle_\pm^2)+\frac{1}{2}\lambda\langle\varepsilon_1+\varepsilon_2+\varepsilon_3\rangle_\pm^2 \]

事实上，分解形式2与分解形式1是一致的

证明2

由式(41)所定义的拉伸、压缩应变能密度，显然满足式(18b)。

偏导数2

\[ \tag{42} \partial_\boldsymbol{\varepsilon}\psi^\pm=2\mu\sum_{i=1}^3 \langle\varepsilon_i\rangle_\pm\boldsymbol{n}_i\otimes\boldsymbol{n}_i+\lambda\langle\varepsilon_1+\varepsilon_2+\varepsilon_3\rangle_\pm\boldsymbol{I} \]

分解形式3

文献[3]中将应变张量 \(\boldsymbol{\varepsilon}\) 分解为球形部分和偏斜部分，即

\[ \tag{43} \begin{cases} \boldsymbol{\varepsilon}_\mathrm{v}=\displaystyle\frac{1}{3}\mathrm{tr}(\boldsymbol{\varepsilon})\boldsymbol{I}\\[5pt] \boldsymbol{\varepsilon}_\mathrm{d}=\boldsymbol{\varepsilon}-\boldsymbol{\varepsilon}_\mathrm{v} \end{cases} \]

于是，在上述分解的基础上定义拉伸应变张量 \(\boldsymbol{\varepsilon}^+\) 与压缩应变张量 \(\boldsymbol{\varepsilon}^-\)

\[ \tag{44} \begin{cases} \boldsymbol{\varepsilon}^+=\boldsymbol{\varepsilon}^+_\mathrm{v}+\boldsymbol{\varepsilon}_\mathrm{d}\\[5pt] \boldsymbol{\varepsilon}^-=\boldsymbol{\varepsilon}^-_\mathrm{v} \end{cases} \]

式中，\(\boldsymbol{\varepsilon}^+_\mathrm{v}=\displaystyle\frac{1}{3}\langle\mathrm{tr}(\boldsymbol{\varepsilon})\rangle_+\boldsymbol{I}~~,~~\boldsymbol{\varepsilon}^-_\mathrm{v}=\frac{1}{3}\langle\mathrm{tr}(\boldsymbol{\varepsilon})\rangle_-\boldsymbol{I}\) 。直接将式(44)所定义的拉伸、压缩应变 \(\boldsymbol{\varepsilon}^+\)、\(\boldsymbol{\varepsilon}^-\) 代入式(16)，令

\[ \tag{45} \begin{cases} \psi^+=\psi(\boldsymbol{\varepsilon}^+)=\mu\boldsymbol{\varepsilon}^+:\boldsymbol{\varepsilon}^++\displaystyle\frac{1}{2}\lambda\mathrm{tr}^2(\boldsymbol{\varepsilon}^+)\\[5pt] \psi^-=\psi(\boldsymbol{\varepsilon}^-)=\mu\boldsymbol{\varepsilon}^-:\boldsymbol{\varepsilon}^-+\displaystyle\frac{1}{2}\lambda\mathrm{tr}^2(\boldsymbol{\varepsilon}^-) \end{cases} \]

证明3

当 \(\mathrm{tr}(\boldsymbol{\varepsilon})>0\) 时，\(\boldsymbol{\varepsilon}^+=\boldsymbol{\varepsilon}\)，\(\boldsymbol{\varepsilon}^-=\boldsymbol{0}\) 。于是 \(\psi^+=\psi(\boldsymbol{\varepsilon})\)，\(\psi^-=0\)，显然满足式(18b)。

当 \(\mathrm{tr}(\boldsymbol{\varepsilon})<0\) 时，\(\boldsymbol{\varepsilon}^+=\boldsymbol{\varepsilon}_\mathrm{d}\)，\(\boldsymbol{\varepsilon}^-=\boldsymbol{\varepsilon}_\mathrm{v}\)。于是 \(\psi^+=\psi(\boldsymbol{\varepsilon}_\mathrm{d})\)，\(\psi^-=\psi(\boldsymbol{\varepsilon}_\mathrm{v})\) 。

在《弹性体的应变能密度》中给出畸变能密度 \(\psi_\mathrm{d}\) 与体积改变能密度 \(\psi_\mathrm{v}\)

\[ \tag{46} \begin{cases} \psi_\mathrm{d}=\psi(\boldsymbol{\varepsilon}_\mathrm{d})=\mu\big[\boldsymbol{\varepsilon}:\boldsymbol{\varepsilon}-\displaystyle\frac{1}{3}\mathrm{tr}^2(\boldsymbol{\varepsilon})\big]\\[5pt] \psi_\mathrm{v}=\psi(\boldsymbol{\varepsilon}_\mathrm{v})=\displaystyle\frac{1}{6}(2\mu+3\lambda)\mathrm{tr}^2(\boldsymbol{\varepsilon}) \end{cases} \]

且 \(\psi_\mathrm{d}+\psi_\mathrm{v}=\psi\)，于是满足式(18b)。

综上，由式(45)所定义的拉伸、压缩应变能密度满足式(18b)。

偏导数3

\(\psi_\mathrm{d}\)、\(\psi_\mathrm{v}\) 对 \(\boldsymbol{\varepsilon}\) 的偏导数 \(\partial_\boldsymbol{\varepsilon}\psi_\mathrm{d}\)、\(\partial_\boldsymbol{\varepsilon}\psi_\mathrm{v}\)

\[ \tag{47} \begin{cases} \partial_\boldsymbol{\varepsilon}\psi_\mathrm{d}=\mu\big[2\boldsymbol{\varepsilon}-\displaystyle\frac{2}{3}\mathrm{tr}(\boldsymbol{\varepsilon})\boldsymbol{I}\big]=2\mu\boldsymbol{\varepsilon}_\mathrm{d}\\[5pt] \partial_\boldsymbol{\varepsilon}\psi_\mathrm{v}=\displaystyle\frac{1}{3}(2\mu+3\lambda)\mathrm{tr}(\boldsymbol{\varepsilon})\boldsymbol{I}=(2\mu+3\lambda)\boldsymbol{\varepsilon}_\mathrm{v} \end{cases} \]

于是有

\[ \tag{48} \begin{cases} \partial_\boldsymbol{\varepsilon}\psi^+=\displaystyle\frac{1}{3}(2\mu+3\lambda)\langle\mathrm{tr}(\boldsymbol{\varepsilon})\rangle_+\boldsymbol{I}+2\mu\boldsymbol{\varepsilon}_\mathrm{d}\\[5pt] \partial_\boldsymbol{\varepsilon}\psi^-=\displaystyle\frac{1}{3}(2\mu+3\lambda)\langle\mathrm{tr}(\boldsymbol{\varepsilon})\rangle_-\boldsymbol{I} \end{cases} \]

参考文献

[1] Miehe C , Welschinger F , Hofacker M . Thermodynamically consistent phase-field models of fracture: Variational principles and multi-field FE implementations[J]. International Journal for Numerical Methods in Engineering, 2010, 83(10):1273-1311.

[2] Hofacker M , Miehe C . Continuum phase field modeling of dynamic fracture: variational principles and staggered FE implementation[J]. International Journal of Fracture, 2012, 178(1-2):p.113-129.

[3] Amor H , Marigo J J , Maurini C . Regularized formulation of the variational brittle fracture with unilateral contact: Numerical experiments[J]. Journal of the Mechanics & Physics of Solids, 2009, 57(8):1209-1229.